The abacus (plural abaci or abacuses), also called a counting frame, is a calculating tool that was in use in Europe, China and Russia, centuries before the adoption of the written Hindu–Arabic numeral system. The exact origin of the abacus is still unknown. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of wood, stone, or metal. Abaci come in different designs. Some designs, like the bead frame consisting of beads divided into tens, are used mainly to teach arithmetic, although they remain popular in the post-Soviet states as a tool. Other designs, such as the Japanese soroban, have been used for practical calculations even involving several digits. For any particular abacus design, there usually are numerous different methods to perform a certain type of calculation, which may include basic operations like addition and multiplication, or even more complex ones, such as calculating square roots. Some of these methods may work with non-natural numbers (numbers such as 1.5 and  3⁄4). Although today many use calculators and computers instead of abaci to calculate, abaci still remain in common use in some countries. Merchants, traders and clerks in some parts of Eastern Europe, Russia, China and Africa use abaci, and they are still used to teach arithmetic to children. Some people who are unable to use a calculator because of visual impairment may use an abacus.

In applied mechanics, bending (also known as flexure) characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically 1/10 or less, of the other two. When the length is considerably longer than the width and the thickness, the element is called a beam. For example, a closet rod sagging under the weight of clothes on clothes hangers is an example of a beam experiencing bending. On the other hand, a shell is a structure of any geometric form where the length and the width are of the same order of magnitude but the thickness of the structure (known as the 'wall') is considerably smaller. A large diameter, but thin-walled, short tube supported at its ends and loaded laterally is an example of a shell experiencing bending. In the absence of a qualifier, the term bending is ambiguous because bending can occur locally in all objects. Therefore, to make the usage of the term more precise, engineers refer to a specific object such as; the bending of rods, the bending of beams, the bending of plates, the bending of shells and so on.

In probability theory and statistics, a central moment is a moment of a probability distribution of a random variable about the random variable's mean; that is, it is the expected value of a specified integer power of the deviation of the random variable from the mean. The various moments form one set of values by which the properties of a probability distribution can be usefully characterised. Central moments are used in preference to ordinary moments, computed in terms of deviations from the mean instead of from zero, because the higher-order central moments relate only to the spread and shape of the distribution, rather than also to its location. Sets of central moments can be defined for both univariate and multivariate distributions.

In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) directed away from the axis of rotation that appears to act on all objects when viewed in a rotating frame of reference. The concept of the centrifugal force can be applied in rotating devices, such as centrifuges, centrifugal pumps, centrifugal governors, and centrifugal clutches, and in centrifugal railways, planetary orbits and banked curves, when they are analyzed in a rotating coordinate system. The term has sometimes also been used for the reactive centrifugal force that is a reaction to a centripetal force.

The Chebychev–Grübler–Kutzbach criterion determines the degree of freedom of a kinematic chain, that is, a coupling of rigid bodies by means of mechanical constraints. These devices are also called linkages. The Kutzbach criterion is also called the mobility formula, because it computes the number of parameters that define the configuration of a linkage from the number of links and joints and the degree of freedom at each joint. Interesting and useful linkages have been designed that violate the mobility formula by using special geometric features and dimensions to provide more mobility than would by predicted by this formula. These devices are called overconstrained mechanisms.

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry.

The electrical resistance of an electrical conductor is a measure of the difficulty to pass an electric current through that conductor. The inverse quantity is electrical conductance, and is the ease with which an electric current passes. Electrical resistance shares some conceptual parallels with the notion of mechanical friction. The SI unit of electrical resistance is the ohm (Ω), while electrical conductance is measured in siemens (S). An object of uniform cross section has a resistance proportional to its resistivity and length and inversely proportional to its cross-sectional area. All materials show some resistance, except for superconductors, which have a resistance of zero. The resistance (R) of an object is defined as the ratio of voltage across it (V) to current through it (I), while the conductance (G) is the inverse: R = V I , G = I V = 1 R {\displaystyle R={V \over I},\qquad G={I \over V}={\frac {1}{R}}} For a wide variety of materials and conditions, V and I are directly proportional to each other, and therefore R and G are constant (although they can depend on other factors like temperature or strain). This proportionality is called Ohm's law, and materials that satisfy it are called ohmic materials. In other cases, such as a diode or battery, V and I are not directly proportional. The ratio V/I is sometimes still useful, and is referred to as a "chordal resistance" or "static resistance", since it corresponds to the inverse slope of a chord between the origin and an I–V curve. In other situations, the derivative d V d I {\displaystyle {\frac {dV}{dI}}\,\!} may be most useful; this is called the "differential resistance".

Fatigue limit, endurance limit, and fatigue strength are all expressions used to describe a property of materials: the amplitude (or range) of cyclic stress that can be applied to the material without causing fatigue failure. Ferrous alloys and titanium alloys have a distinct limit, an amplitude below which there appears to be no number of cycles that will cause failure. Other structural metals such as aluminium and copper do not have a distinct limit and will eventually fail even from small stress amplitudes. In these cases, a number of cycles (usually 107) is chosen to represent the fatigue life of the material. Fatigue limit is used in plotting S-N curves and the Goodman diagram.

Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction: Dry friction is a force that opposes the relative lateral motion of two solid surfaces in contact. Dry friction is subdivided into static friction ("stiction") between non-moving surfaces, and kinetic friction between moving surfaces. With the exception of atomic or molecular friction, dry friction generally arises from the interaction of surface features, known as asperities Fluid friction describes the friction between layers of a viscous fluid that are moving relative to each other. Lubricated friction is a case of fluid friction where a lubricant fluid separates two solid surfaces. Skin friction is a component of drag, the force resisting the motion of a fluid across the surface of a body. Internal friction is the force resisting motion between the elements making up a solid material while it undergoes deformation. When surfaces in contact move relative to each other, the friction between the two surfaces converts kinetic energy into thermal energy (that is, it converts work to heat). This property can have dramatic consequences, as illustrated by the use of friction created by rubbing pieces of wood together to start a fire. Kinetic energy is converted to thermal energy whenever motion with friction occurs, for example when a viscous fluid is stirred. Another important consequence of many types of friction can be wear, which may lead to performance degradation or damage to components. Friction is a component of the science of tribology. Friction is desirable and important in supplying traction to facilitate motion on land. Most land vehicles rely on friction for acceleration, deceleration and changing direction. Sudden reductions in traction can cause loss of control and accidents. Friction is not itself a fundamental force. Dry friction arises from a combination of inter-surface adhesion, surface roughness, surface deformation, and surface contamination. The complexity of these interactions makes the calculation of friction from first principles impractical and necessitates the use of empirical methods for analysis and the development of theory. Friction is a non-conservative force - work done against friction is path dependent. In the presence of friction, some energy is always lost in the form of heat. Thus mechanical energy is not conserved.

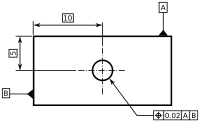
Geometric Dimensioning and Tolerancing (GD&T) is a system for defining and communicating engineering tolerances. It uses a symbolic language on engineering drawings and computer-generated three-dimensional solid models that explicitly describes nominal geometry and its allowable variation. It tells the manufacturing staff and machines what degree of accuracy and precision is needed on each controlled feature of the part. GD&T is used to define the nominal (theoretically perfect) geometry of parts and assemblies, to define the allowable variation in form and possible size of individual features, and to define the allowable variation between features. Dimensioning specifications define the nominal, as-modeled or as-intended geometry. One example is a basic dimension. Tolerancing specifications define the allowable variation for the form and possibly the size of individual features, and the allowable variation in orientation and location between features. Two examples are linear dimensions and feature control frames using a datum reference (both shown above). There are several standards available worldwide that describe the symbols and define the rules used in GD&T. One such standard is American Society of Mechanical Engineers (ASME) Y14.5-2009. This article is based on that standard, but other standards, such as those from the International Organization for Standardization (ISO), may vary slightly. The Y14.5 standard has the advantage of providing a fairly complete set of standards for GD&T in one document. The ISO standards, in comparison, typically only address a single topic at a time. There are separate standards that provide the details for each of the major symbols and topics below (e.g. position, flatness, profile, etc.).