Login
Our 3D CAD supplier models have been moved to 3Dfindit.com, the new visual search engine for 3D CAD, CAE & BIM models.
You can log in there with your existing account of this site.
The content remains free of charge.

Top Links
Knowledge Contributors
Search
Favorite Knowledge
Knowledge
Knowledge - 235 Items
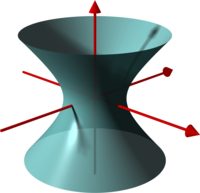
Hyperboloid ( 17699 views )
Hyperboloid
In geometry, a hyperboloid of revolution, sometimes called circular hyperboloid, is a surface that may be generated by rotating a hyperbola around one of its principal axes. An hyperboloid is a surface that may be obtained from a paraboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.
A hyperboloid is a quadric surface, that is a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has also three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry.
Given a hyperboloid, if one chooses a Cartesian coordinate system whose axes are axes of symmetry of the hyperboloid, and origin is the center of symmetry of the hyperboloid, then the hyperboloid may be defined by one of the two following equations:
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
1
,
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1,}
or
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
−
1.
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1.}
Both of these surfaces are asymptotic to the cone of equation
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
0.
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0.}
One has an hyperboloid of revolution if and only if
a
2
=
b
2
.
{\displaystyle a^{2}=b^{2}.}
Otherwise, the axes are uniquely defined (up to the exchange of the x-axis and the y-axis.
There are two kinds of hyperboloids. In the first case (+1 in the right-hand side of the equation), one has a one-sheet hyperboloid, also called hyperbolic hyperboloid. It is a connected surface, which has a negative Gaussian curvature at every point. This implies that the tangent plane at any point intersect the hyperboloid into two lines, and thus that the one-sheet hyperboloid is a doubly ruled surface.
In the second case (−1 in the right-hand side of the equation), one has a two-sheet hyperboloid, also called elliptic hyperboloid. The surface has two connected components, and a positive Gaussian curvature at every point. Thus the surface is convex in the sense that the tangent plane at every point intersects the surface only in this point.
Hyperloop ( 10040 views )
Hyperloop
Licensed under Creative Commons Attribution-Share Alike 4.0 (Camilo Sanchez).
A Hyperloop is a proposed mode of passenger and/or freight transportation, first used to describe an open-source vactrain design released by a joint team from Tesla and SpaceX. Drawing heavily from Robert Goddard's vactrain, a hyperloop comprises a sealed tube or system of tubes through which a pod may travel free of air resistance or friction conveying people or objects at high speed while being very efficient.
Elon Musk's version of the concept, first publicly mentioned in 2012, incorporates reduced-pressure tubes in which pressurized capsules ride on air bearings driven by linear induction motors and air compressors.
The Hyperloop Alpha concept was first published in August 2013, proposing and examining a route running from the Los Angeles region to the San Francisco Bay Area roughly following the Interstate 5 corridor. The paper conceived of a hyperloop system that would propel passengers along the 350-mile (560 km) route at an average speed of around 600 mph (970 km/h), with a top speed of 760 mph (1,200 km/h), allowing for a travel time of 35 minutes, which is considerably faster than current rail or air travel times. Preliminary cost estimates for this LA–SF suggested route were included in the white paper—US$6 billion for a passenger-only version, and US$7.5 billion for a somewhat larger-diameter version transporting passengers and vehicles—although transportation analysts had doubts that the system could be constructed on that budget; some analysts claimed that the Hyperloop would be several billion dollars overbudget, taking into consideration construction, development and operation costs.
The Hyperloop concept has been explicitly "open-sourced" by Musk and SpaceX, and others have been encouraged to take the ideas and further develop them.
To that end, a few companies have been formed, and several interdisciplinary student-led teams are working to advance the technology. SpaceX built an approximately 1-mile-long (1.6 km) subscale track for its pod design competition at its headquarters in Hawthorne, California.
Some experts are skeptical, saying that the proposals ignore the expenses and risks of developing the technology and that the idea is "completely impractical". Claims have also been made that the Hyperloop is too susceptible to disruption from a power outage or terror attacks to be considered safe.
Hypotenuse ( 9615 views )
Hypotenuse
Licensed under Creative Commons Attribution-Share Alike 3.0 (Dmcq).
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite of the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides.
For example, if one of the other sides has a length of 3 (when squared, 9) and the other has a length of 4 (when squared, 16), then their squares add up to 25. The length of the hypotenuse is the square root of 25, that is, 5.
Hyundai Motor Company ( 27783 views )
Hyundai Motor Company
The Hyundai Motor Company (Hangul: 현대자동차; Hanja: 現代自動車; RR: Hyeondae Jadongcha listen; Hangul: 현대; Hanja: 現代; MR: Hyŏndae, IPA: [hjə́ːndɛ], modernity; KRX: 005380) is a South Korean multinational automotive manufacturer headquartered in Seoul, South Korea. The company was founded in 1967 and, along with its 32.8% owned subsidiary, Kia Motors, and its 100% owned luxury subsidiary Genesis Motors which together comprise the Hyundai Motor Group. It is the third largest vehicle manufacturer in the world.
Hyundai operates the world's largest integrated automobile manufacturing facility in Ulsan, South Korea, which has an annual production capacity of 1.6 million units. The company employs about 75,000 people worldwide. Hyundai vehicles are sold in 193 countries through some 5,000 dealerships and showrooms.