Login
Our 3D CAD supplier models have been moved to 3Dfindit.com, the new visual search engine for 3D CAD, CAE & BIM models.
You can log in there with your existing account of this site.
The content remains free of charge.

Top Links
Knowledge Contributors
Search
Favorite Knowledges
|
22.751 |
Fractal |
|
20.491 |
Classical mechanics |
|
19.478 |
Voronoi diagram |
|
17.672 |
Molecule |
|
15.659 |
Polyatomic ion |
|
12.874 |
Roll-on/roll-off |
|
12.132 |
Encryption |
|
10.163 |
Durga |
|
8.014 |
Secure communication |
|
1.824 |
VersaLogic |
Knowledge
Knowledge - 10 Items
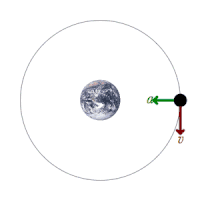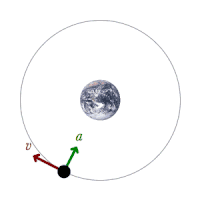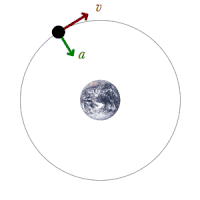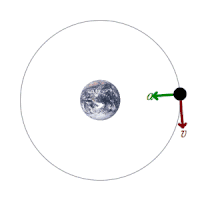
Classical mechanics ( 20491 views )
Classical mechanics
Licensed under Creative Commons Attribution-Share Alike 4.0 (Own work).
Classical mechanics describes the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars and galaxies.
If the present state of an object is known it is possible to predict by the laws of classical mechanics how it will move in the future (determinism) and how it has moved in the past (reversibility).
The earliest development of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts employed by and the mathematical methods invented by Isaac Newton and Gottfried Wilhelm Leibniz and others in the 17th century to describe the motion of bodies under the influence of a system of forces.
Later, more abstract methods were developed, leading to the reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advances, made predominantly in the 18th and 19th centuries, extend substantially beyond Newton's work, particularly through their use of analytical mechanics. They are, with some modification, also used in all areas of modern physics.
Classical mechanics provides extremely accurate results when studying large objects that are not extremely massive and speeds not approaching the speed of light. When the objects being examined have about the size of an atom diameter, it becomes necessary to introduce the other major sub-field of mechanics: quantum mechanics. To describe velocities that are not small compared to the speed of light, special relativity is needed. In case that objects become extremely massive, general relativity becomes applicable. However, a number of modern sources do include relativistic mechanics into classical physics, which in their view represents classical mechanics in its most developed and accurate form.
Durga ( 10163 views )
Durga
Durga (Sanskrit: दुर्गा, IAST: Durgā), identified as Adi Parashakti, is a principal and popular form of Hindu Goddess. She is the warrior goddess, whose mythology centres around combating evils and demonic forces that threaten peace, prosperity and dharma of the good. She is the fierce form of the protective mother goddess, willing to unleash her anger against wrong, violence for liberation and destruction to empower creation.Durga is depicted in the Hindu pantheon as a Goddess riding a lion or tiger, with many arms each carrying a weapon, often defeating Mahishasura (lit. buffalo demon).
The three principle forms of Durga worshiped are Maha Durga, Chandika and Aparajita. Of these, Chandika has two forms called Chandi who is of the combined power and form of Saraswati, Lakshmi and Parvati and of Chamunda who is a form of Kali created by the goddess for killing demons Chanda and Munda. Maha Durga has three forms: Ugrachanda, Bhadrakali and Katyayani. Bhadrakali Durga is also worshiped in the form of her nine epithets called Navadurga.
She is a central deity in Shaktism tradition of Hinduism, where she is equated with the concept of ultimate reality called Brahman. One of the most important texts of Shaktism is Devi Mahatmya, also known as Durgā Saptashatī or Chandi patha, which celebrates Durga as the goddess, declaring her as the supreme being and the creator of the universe. Estimated to have been composed between 400 and 600 CE, this text is considered by Shakta Hindus to be as important a scripture as the Bhagavad Gita. She has a significant following all over India, Bangladesh and Nepal, particularly in its eastern states such as West Bengal, Odisha, Jharkhand, Assam and Bihar. Durga is revered after spring and autumn harvests, specially during the festival of Navratri.
Encryption ( 12132 views )
Encryption
In cryptography, encryption is the process of encoding a message or information in such a way that only authorized parties can access it and those who are not authorized cannot. Encryption does not itself prevent interference, but denies the intelligible content to a would-be interceptor. In an encryption scheme, the intended information or message, referred to as plaintext, is encrypted using an encryption algorithm – a cipher – generating ciphertext that can be read only if decrypted. For technical reasons, an encryption scheme usually uses a pseudo-random encryption key generated by an algorithm. It is in principle possible to decrypt the message without possessing the key, but, for a well-designed encryption scheme, considerable computational resources and skills are required. An authorized recipient can easily decrypt the message with the key provided by the originator to recipients but not to unauthorized users.
Fractal ( 22751 views )
Fractal
Licensed under GNU General Public License (Unkown).
In mathematics, a fractal is a detailed, recursive, and infinitely self-similar mathematical set whose Hausdorff dimension strictly exceeds its topological dimension. Fractals are encountered ubiquitously in nature due to their tendency to appear nearly the same at different levels, as is illustrated here in the successively small magnifications of the Mandelbrot set. Fractals exhibit similar patterns at increasingly small scales, also known as expanding symmetry or unfolding symmetry; If this replication is exactly the same at every scale, as in the Menger sponge, it is called a self-similar pattern.
One way that fractals are different from finite geometric figures is the way in which they scale. Doubling the edge lengths of a polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the dimension of the space the polygon resides in). Likewise, if the radius of a sphere is doubled, its volume scales by eight, which is two (the ratio of the new to the old radius) to the power of three (the dimension that the sphere resides in). However, if a fractal's one-dimensional lengths are all doubled, the spatial content of the fractal scales by a power that is not necessarily an integer. This power is called the fractal dimension of the fractal, and it usually exceeds the fractal's topological dimension.As mathematical equations, fractals are usually nowhere differentiable. An infinite fractal curve can be conceived of as winding through space differently from an ordinary line - although it is still 1-dimensional its fractal dimension indicates that it also resembles a surface.
The mathematical roots of fractals have been traced throughout the years as a formal path of published works, starting in the 17th century with notions of recursion, then moving through increasingly rigorous mathematical treatment of the concept to the study of continuous but not differentiable functions in the 19th century by the seminal work of Bernard Bolzano, Bernhard Riemann, and Karl Weierstrass, and on to the coining of the word fractal in the 20th century with a subsequent burgeoning of interest in fractals and computer-based modelling in the 20th century. The term "fractal" was first used by mathematician Benoit Mandelbrot in 1975. Mandelbrot based it on the Latin frāctus meaning "broken" or "fractured", and used it to extend the concept of theoretical fractional dimensions to geometric patterns in nature.There is some disagreement amongst authorities about how the concept of a fractal should be formally defined. Mandelbrot himself summarized it as "beautiful, damn hard, increasingly useful. That's fractals." More formally, in 1982 Mandelbrot stated that "A fractal is by definition a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension." Later, seeing this as too restrictive, he simplified and expanded the definition to: "A fractal is a shape made of parts similar to the whole in some way." Still later, Mandelbrot settled on this use of the language: "...to use fractal without a pedantic definition, to use fractal dimension as a generic term applicable to all the variants."The consensus is that theoretical fractals are infinitely self-similar, iterated, and detailed mathematical constructs having fractal dimensions, of which many examples have been formulated and studied in great depth. Fractals are not limited to geometric patterns, but can also describe processes in time. Fractal patterns with various degrees of self-similarity have been rendered or studied in images, structures and sounds and found in nature, technology, art, architecture and law. Fractals are of particular relevance in the field of chaos theory, since the graphs of most chaotic processes are fractals.
Molecule ( 17672 views )
Molecule
Licensed under Creative Commons Attribution 4.0 (Kota Iwata et al.).
A molecule is an electrically neutral group of two or more atoms held together by chemical bonds. Molecules are distinguished from ions by their lack of electrical charge. However, in quantum physics, organic chemistry, and biochemistry, the term molecule is often used less strictly, also being applied to polyatomic ions.
In the kinetic theory of gases, the term molecule is often used for any gaseous particle regardless of its composition. According to this definition, noble gas atoms are considered molecules as they are monatomic molecules.A molecule may be homonuclear, that is, it consists of atoms of one chemical element, as with oxygen (O2); or it may be heteronuclear, a chemical compound composed of more than one element, as with water (H2O). Atoms and complexes connected by non-covalent interactions, such as hydrogen bonds or ionic bonds, are generally not considered single molecules.Molecules as components of matter are common in organic substances (and therefore biochemistry). They also make up most of the oceans and atmosphere. However, the majority of familiar solid substances on Earth, including most of the minerals that make up the crust, mantle, and core of the Earth, contain many chemical bonds, but are not made of identifiable molecules. Also, no typical molecule can be defined for ionic crystals (salts) and covalent crystals (network solids), although these are often composed of repeating unit cells that extend either in a plane (such as in graphene) or three-dimensionally (such as in diamond, quartz, or sodium chloride). The theme of repeated unit-cellular-structure also holds for most condensed phases with metallic bonding, which means that solid metals are also not made of molecules. In glasses (solids that exist in a vitreous disordered state), atoms may also be held together by chemical bonds with no presence of any definable molecule, nor any of the regularity of repeating units that characterizes crystals.
Polyatomic ion ( 15659 views )
Polyatomic ion
A polyatomic ion, also known as a molecular ion, is a charged chemical species (ion) composed of two or more atoms covalently bonded or of a metal complex that can be considered to be acting as a single unit. The prefix poly- means "many," in Greek, but even ions of two atoms are commonly referred to as polyatomic. In older literature, a polyatomic ion is also referred to as a radical, and less commonly, as a radical group. In contemporary usage, the term radical refers to free radicals that are (not necessarily charged) species with an unpaired electron.
An example of a polyatomic ion is the hydroxide ion; consisting of one oxygen atom and one hydrogen atom, hydroxide has a charge of −1. Its chemical formula is OH−. An ammonium ion is made up of one nitrogen atom and four hydrogen atoms: it has a charge of +1, and its chemical formula is NH+4.
Polyatomic ions are often useful in the context of acid-base chemistry or in the formation of salts. A polyatomic ion can often be considered as the conjugate acid/base of a neutral molecule. For example, the conjugate base of sulfuric acid (H2SO4) is the polyatomic hydrogen sulfate anion (HSO−4). The removal of another hydrogen ion yields the sulfate anion (SO2−4).
Roll-on/roll-off ( 12874 views )
Roll-on~roll-off
Licensed under Creative Commons Attribution-Share Alike 3.0 (Unkown).
Roll-on/roll-off (RORO or ro-ro) ships are vessels designed to carry wheeled cargo, such as cars, trucks, semi-trailer trucks, trailers, and railroad cars, that are driven on and off the ship on their own wheels or using a platform vehicle, such as a self-propelled modular transporter. This is in contrast to lift-on/lift-off (LoLo) vessels, which use a crane to load and unload cargo.
RORO vessels have either built-in or shore-based ramps that allow the cargo to be efficiently rolled on and off the vessel when in port. While smaller ferries that operate across rivers and other short distances often have built-in ramps, the term RORO is generally reserved for large oceangoing vessels. The ramps and doors may be located in stern, bow or sides, or any combination thereof.
Secure communication ( 8014 views )
Secure communication
Secure communication is when two entities are communicating and do not want a third party to listen in. For that they need to communicate in a way not susceptible to eavesdropping or interception. Secure communication includes means by which people can share information with varying degrees of certainty that third parties cannot intercept what was said. Other than spoken face-to-face communication with no possible eavesdropper, it is probably safe to say that no communication is guaranteed secure in this sense, although practical obstacles such as legislation, resources, technical issues (interception and encryption), and the sheer volume of communication serve to limit surveillance.
With many communications taking place over long distance and mediated by technology, and increasing awareness of the importance of interception issues, technology and its compromise are at the heart of this debate. For this reason, this article focusses on communications mediated or intercepted by technology.
Also see Trusted Computing, an approach under present development that achieves security in general at the potential cost of compelling obligatory trust in corporate and government bodies.
VersaLogic ( 1824 views )
VersaLogic
VersaLogic is a privately held corporation located in Tualatin, Oregon, USA that designs and manufactures board-level products for embedded systems. The company's products are used by OEMs in a wide range of markets including medical, transportation, security, instrumentation, robotics, avionics, and unmanned vehicles.
Voronoi diagram ( 19478 views )
Voronoi diagram
Licensed under Creative Commons Attribution-Share Alike 4.0 (Balu Ertl).
In mathematics, a Voronoi diagram is a partitioning of a plane into regions based on distance to points in a specific subset of the plane. That set of points (called seeds, sites, or generators) is specified beforehand, and for each seed there is a corresponding region consisting of all points closer to that seed than to any other. These regions are called Voronoi cells. The Voronoi diagram of a set of points is dual to its Delaunay triangulation.
It is named after Georgy Voronoi, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). Voronoi diagrams have practical and theoretical applications in a large number of fields, mainly in science and technology, but also in visual art. They are also known as Thiessen polygons.